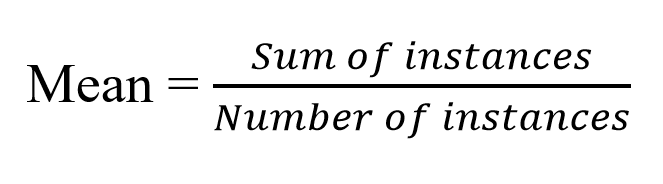Published: Feb 11, 2025

that translated to:

Median: The Middle Value - "The Fair Middle"

The median is another way to find the “center” of the data, but instead of averaging everything, we arrange the values in ascending order and find the middle number. If there’s an even number of values, we take the average of the two middle numbers.

Sorted weights: [22, 23, 24, 24, 26, 28, 28, 29, 30, 33]

Since we have an even number of values (10), the two middle numbers are 26 and 28. Their average gives us the median:

Median = (26 + 28) / 2 = 27 grams

Mode: The Most Frequent Value - "The Most Common One"

The mode is the most common value in the dataset. Looking at our mice weights again, we see that 24 and 28 each appear twice, while all other numbers appear only once.

Since we have two values appearing most frequently, we say this dataset has two modes (24 and 28).

Great Now What ?

At this point, you might be thinking: “Cool, but why does this matter? Why would I ever care about the mean, median, or mode of a group of mice?”

Well, as my friend “Digga” would say: Now you have an estimation of what your group of mice looks like. daaa

That’s useful, but let’s push it further. If the mean weight of your mice was 35 grams instead of 26.7 grams, that would indicate they’re much heavier than average, perhaps overweight. With this simple calculation, you already have an insight into the general condition of your group. And in other real-world scenarios, like analyzing salaries, house prices, or patient health data, these three measures can help make sense of large datasets quickly.

Manufacturing Quality Control: Mean vs. Median

Let’s say we have this Scenario: A factory produces bottles of juice and needs to ensure each bottle contains 500 mL of juice.

Using the Mean: The company measures 100 bottles and finds the average (mean) volume is 500 mL.

Sounds good, right? But if some bottles have 480 mL and others have 520 mL, customers will complain.

But when the Median: The company checks the median and finds it’s 495 mL.

This means thefirst half the bottles have less than 495 mL, which is a problem. Even though the mean says "everything is fine," most customers get underfilled bottles!

Decision: The company adjusts the filling machine to center around 500 mL (median) rather than relying only on the mean.

Detecting Anomalies in Production: Mean vs. Mode

Scenario: A car factory measures the diameter of brake discs to ensure they meet the standard of 30 cm.

Mean diameter: 30.2 cm

Mode diameter: 30 cm

The mean is slightly off, but the mode shows most discs are actually correct.

A few faulty discs (e.g., 32 cm) pushed up the mean.

Decision:

• The factory doesn’t panic because the mode shows most discs are fine.

• However, they inspect outliers to prevent defective discs from reaching customers.

Sales Analysis: Mean vs. Mode

Scenario: A retailer sells smartphones and wants to decide which price range to focus on.

Mean selling price: €750

Mode (Most common selling price): €500

The mean is inflated because some customers buy high-end €1,500 phones.

The mode tells them that most customers buy €500 phones.

Decision:

Instead of pushing expensive phones, they increase stock and promotions for €500 models to match customer demand.


Useful Links:

• Josh Starmer —> (3117) Statistics Fundamentals - YouTube

• Practical Statistics for Data Scientists by Peter Bruce, Andrew Bruce